Crystal building in Atomes
The crystal building process in Atomes will be briefly presented in the next pages. 2 example cases will be used to illustrate the methodology implemented in the program:
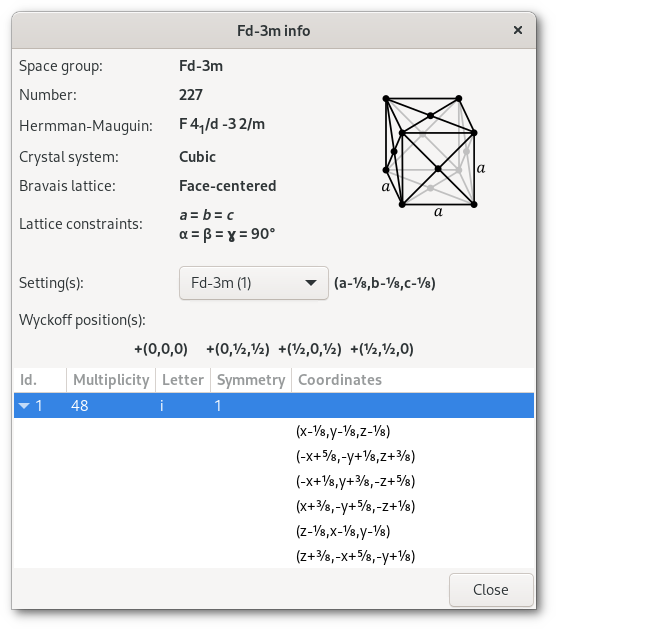
The Fd\(\bar{3}\)m space group, N\(^\circ\)227, with the first setting: origin 1.
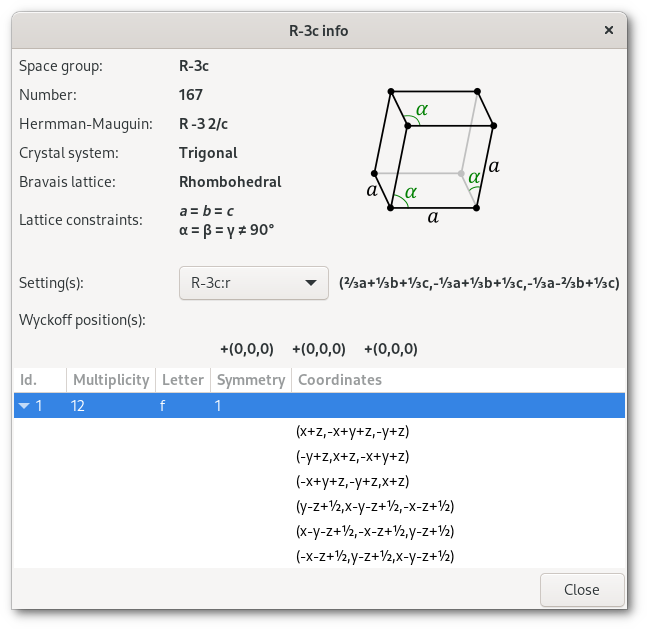
The R\(\bar{3}\)c space group, N\(^\circ\)167, with the second setting: rhombohedral parameters.
The terminology used in the Atomes program, and therefore used in this manual, is directly taken from the International tables for Crystallography Vol. A. [1]
In the following every single step depends on the considered space group, and corresponds to the way the process is implemented in Atomes:
Determine the origin of the coordinate system.
Calculate the inverse transformation matrix.
Select the space group extra site positions, if any.
Adjust the different symmetrical positions of the first Wyckoff position using [cb:2].
Calculate the crystalline positions using [cb:4] and [cb:3].
Select the unique position(s) in [cb:5] to build the crystal.
Calculate the object position in Cartesian coordinates using [cb:6].
Insert object(s) at the appropriate coordinates based on occupancy.
Origin of the coordinate system
The origin of the coordinate system, if any particular, determine how the object fractional coordinates are modified to match the space group criteria before calculating the Cartesian coordinates. The first step is to build the 4\(\times\)3 matrix that describe the operation of be performed, the required information is given by the space group setting, the easiest way to use it is on the form of the transformation matrix P:
Ex: (a, b, c) and can be converted in:
\[\left[\begin{array}{rrrr} 1 & 0 & 0 & \quad 0 \\ 0 & 1 & 0 & \quad 0 \\ 0 & 0 & 1 & \quad 0 \end{array}\right]\]
| (1) Fd\(\bar{3}\)m space group, N\(^\circ\)227, origin 1: | (2) R\(\bar{3}\)c space group, N\(^\circ\)167, second setting: | |
 |  | |
| (a-\(\frac{1}{8}\), b-\(\frac{1}{8}\), c-\(\frac{1}{8}\)) | (\(\frac{2}{3}\)a+\(\frac{1}{3}\)b+\(\frac{1}{3}\)c, \(-\frac{1}{3}\)a+\(\frac{1}{3}\)b+\(\frac{1}{3}\)c, \(-\frac{1}{3}\)a-\(\frac{2}{3}\)b+\(\frac{1}{3}\)c) | |
| The corresponding P matrix are: | ||
| \(\left[\begin{array}{rrrr} 1 & 0 & 0 & \quad -\frac{1}{8} \\ 0 & 1 & 0 & \quad -\frac{1}{8} \\ 0 & 0 & 1 & \quad -\frac{1}{8} \end{array}\right]\) | \(\left[\begin{array}{rrrr} \frac{2}{3} & -\frac{1}{3} & -\frac{1}{3} & \quad 0 \\ \frac{1}{3} & \frac{1}{3} & -\frac{2}{3} & \quad 0 \\ \frac{1}{3} & \frac{1}{3} & \frac{1}{3} & \quad 0 \end{array}\right]\) |
Inverse transformation matrix
To transform the coordinates to the appropriate system we use the corresponding inverse matrix P\(^{-1}\):
| (1) Fd\(\bar{3}\)m space group, N\(^\circ\)227, origin 1: | (2) R\(\bar{3}\)c space group, N\(^\circ\)167, second setting: | |
| \(\left[\begin{array}{rrrr} 1 & 0 & 0 & \quad -\frac{1}{8} \\ 0 & 1 & 0 & \quad -\frac{1}{8} \\ 0 & 0 & 1 & \quad -\frac{1}{8} \end{array}\right]\) | \(\left[\begin{array}{rrrr} 1 & 0 & 1 & \quad 0 \\ -1 & 1 & 1 & \quad 0 \\ 0 & -1 & 1 & \quad 0 \end{array}\right]\) |
The P\(^{-1}\) matrix allows to easily compute the coordinates \((x',y',z')\) of a point \((x,y,z)\) in the appropriate coordinate system using: \[\label{sgconv} (x',y',z') = {\bf{P}}^{-1} \times (x,y,z)\]
Space group extra site position(s)
The space group extra site position(s) describe translations to be performed on the initial set of Wyckoff position to get the entire list of coordinates.
The list of extra position(s), \(E(e_x,e_y,e_z)\), is imported from the space group data file, and is presented on top the Wyckoff positions table of the space group info window:
| (1) Fd\(\bar{3}\)m space group, N\(^\circ\)227, origin 1: | (2) R\(\bar{3}\)c space group, N\(^\circ\)167, second setting: | |
| \(+ (0,0,0) + (0,\frac{1}{2},\frac{1}{2}) + (\frac{1}{2},0,\frac{1}{2}) + (\frac{1}{2},\frac{1}{2},0)\) | \(+ (0,0,0) + (0,0,0) + (0,0,0)\) |
Symmetrical positions using the first Wyckoff position
The first step is to convert the list of coordinates from the first Wyckoff position on the form of matrix W:
| (1) Fd\(\bar{3}\)m space group, N\(^\circ\)227, origin 1: | (2) R\(\bar{3}\)c space group, N\(^\circ\)167, second setting: | |
| (x, y, z) | (x, y, z) | |
| \(\left[\begin{array}{rrrr} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{array}\right]\) | \(\left[\begin{array}{rrrr} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{array}\right]\) |
The W' matrix, suitable for the calculation, is calculated using the P\(^{-1}\) matrix for the corresponding space group: \[{\bf{W'}} = {\bf{W}} \times {\bf{P^{-1}}}\]
| (1) Fd\(\bar{3}\)m space group, N\(^\circ\)227, origin 1: | (2) R\(\bar{3}\)c space group, N\(^\circ\)167, second setting: | |
| \(\left[\begin{array}{rrrr} 1 & 0 & 0 & \quad -\frac{1}{8} \\ 0 & 1 & 0 & \quad -\frac{1}{8} \\ 0 & 0 & 1 & \quad -\frac{1}{8} \end{array}\right]\) | \(\left[\begin{array}{rrrr} 1 & 1 & 0 & \quad 0 \\ -1 & 1 & 1 & \quad 0 \\ 0 & -1 & 1 & \quad 0 \end{array}\right]\) |
The results, converted back to standard coordinates, are presented in the Wyckoff positions table of the space group info window:
| (1) Fd\(\bar{3}\)m space group, N\(^\circ\)227, origin 1: | (2) R\(\bar{3}\)c space group, N\(^\circ\)167, second setting: | |
| \((x - \frac{1}{8}, y - \frac{1}{8}, z - \frac{1}{8})\) | \((x + z, - x + y + z, - y + z)\) | |
| \(\dots\) | \(\dots\) |
Object position(s)
The first step in getting the final fractional coordinates \(F(f_x, f_y, f_z)\) of an object to insert with fractional coordinates given at input \(O(o_x, o_y, o_z)\) is to convert its coordinates to the proper coordinates system \(O'(o_x', o_y', o_z')\): \[O'(o_x', o_y', o_z') = {\bf{P}} \times O(o_x, o_y, o_z)\] Then for a particular Wyckoff position W' and extra site position \(E(x,y,z)\), the final fractional coordinates \(F(f_x, f_y, f_z)\) are calculated by: \[F(f_x, f_y, f_z) = E(e_x,e_y,e_z) + {\bf{W'}} \times O'(o_x', o_y', o_z')\]
Removing duplicate position(s)
Since one of the goal in Atomes is to build crystal structure of super-structure to work with, all crystalline positions cannot be conserved and duplicate positions (same positions using the periodic boundary conditions) must be removed.
When final positions \(F(f_x, f_y, f_z)\) are calculated duplicates are removed on the fly. The first final position with a unique set of coordinates \(F(f_x, f_y, f_z)\) is preserved while the others will be ignored. Duplicates are identical set of atomic coordinates, that can be found because of the symmetrical properties of the space group.
In Atomes a duplicate position \(F_b(b_x, b_y, b_z)\) will be removed if \(F_a(a_x, a_y, a_z)\) has already been found and providing that:
| \(\begin{bmatrix} a_x & = & b_x & \bf{or} & abs(a_x - b_x) & = & n, n \text{ integer} \end{bmatrix}\) | |
| and | \(\begin{bmatrix} a_y & = & b_y & \bf{or} & abs(a_y - b_y) & = & n, n \text{ integer} \end{bmatrix}\) |
| and | \(\begin{bmatrix}a_z & = & b_z & \bf{or} & abs(a_z - b_z) & = & n, n \text{ integer} \end{bmatrix}\) |
Calculate the object final position(s) in Cartesian coordinates
After the construction/selection process Cartesian coordinates \(C(c_x, c_y, c_z)\) of an object with fractional coordinates \(F(f_x, f_y, f_z)\) are calculated using: \[C(c_x, c_y, c_z) = {\bf{FtC}} \times F(f_x, f_y, f_z)\] with FtC the fractional to Cartesian conversion matrix is defined by: \[\begin{bmatrix} \bf{a} & \bf{b}\cos{\gamma} & \bf{c}\cos{\beta} \\ 0 & \bf{b}\sin{\gamma} & \bf{c}\omega \\ 0 & 0 & \frac{\Omega}{\bf{ab}\sin{\gamma}} \end{bmatrix}\] where \(\omega\) and \(\Omega\) are respectively: \[\omega = \frac{\cos{\alpha} - \cos{\beta}\cos{\gamma}}{\sin{\gamma}}\] and: \[\Omega = \bf{abc}\sqrt{1-\cos^2{\alpha} -\cos^2{\beta} -\cos^2{\gamma} + 2\cos{\alpha}\cos{\beta}\cos{\gamma}}\]
a, b, c and \(\alpha\), \(\beta\), \(\gamma\) are the lattice parameters provided at input.
Occupancy
The only thing left to do after that it to select which set of coordinates are to be occupied among the list prepared in the previous steps. Depending on the occupancy defined at input Atomes does the following:
If the occupancy is equal to 1.0: all coordinates are to be occupied and no particular selection is performed.
If the occupancy is < 1.0, then the following options are possible to handle occupancy:
"
Random for the initial cell only": sites are filled randomly in the initial cell only, then the initial cell is simply replicated."
Random cell by cell": sites are filled randomly for each cell, cell by cell separately."
Completely random": sites are filled randomly for the entire network, the final crystal is considered as whole."
Successively": sites are filled successively, all object(s) A are inserted (for the first \(n(A)\) positions), then all object(s) B are inserted (for the next \(n(B)\) positions) ..."
Alternatively": sites are filled alternatively: object A is inserted on the first position, object B is inserted on the second position, object A on the third position, object B on the fourth position ... and so on.
For [i], [ii], [iv] and [v] the number of object(s) by cell is constant, but it can vary for [iii].
For [iv] and [v] the order of the positions to be filled is the order they are found in during the previous steps.
Final check: distance(s) between inserted objects
Finally the last calculation performed by Atomes when creating the crystal is distance check between the object(s) be inserted. Note that this check performed, if and only if, no overlapping is allowed.
If any distance \(d_{ab}\) between 2 objects a and b, is found to be too small the following can happen:
If \(d_{ab} < 0.5\) Å then a warning message will pop-up and ask for the user confirmation to continue, or not, to build the crystal.
If the user decides to build the crystal anyway and if \(d_{ab} = 0.0\) then for fail safe reasons object \(b\) is removed from the list to build.
The "SGL" "Space group info XML file" format
The data files that contain the information regarding each of the 230 space groups are located in the "bin/library/space_groups" directory.
In this folder to each space group corresponds a file with a name following the construction:
"space group number"-"space group name"."sgl"
For the Fd\(\bar{3}\)m space group, the corresponding file is "227-Fd-3m.sgl".
These files must have the ".sgl" extension, follow the "XML" encoding rules, and the following structure:
<?xml version="1.0" encoding="UTF-8"?>
<!– Space group info XML file –>
<sg-xml>
<space-group>R-3c</space-group>
<sg-num>167</sg-num>
<hm-symbol>R -3 2/c</hm-symbol>
<bravais>Trigonal</bravais>
<settings num="2">
<set name="R_-3_c_:h" x="a" y="b" z="c">
<points num="3">
<pt x="0" y="0" z="0"/>
<pt x="2/3" y="1/3" z="1/3"/>
<pt x="1/3" y="2/3" z="2/3"/>
</points>
</set>
<set name="R_-3_c_:r" x="2/3a+1/3b+1/3c" y="-1/3a+1/3b+1/3c" z="-1/3a-2/3b+1/3c">
<points num="3">
<pt x="0" y="0" z="0"/>
<pt x="0" y="0" z="0"/>
<pt x="0" y="0" z="0"/>
</points>
</set>
</settings>
<wyckoff num="6">
<wyck id="1" mul="12" let="f" site="1">
<pos x="x" y="y" z="z"/>
<pos x="-y" y="x-y" z="z"/>
<pos x="-x+y" y="-x" z="z"/>
<pos x="y" y="x" z="-z+1/2"/>
<pos x="x-y" y="-y" z="-z+1/2"/>
<pos x="-x" y="-x+y" z="-z+1/2"/>
<pos x="-x" y="-y" z="-z"/>
<pos x="y" y="-x+y" z="-z"/>
<pos x="x-y" y="x" z="-z"/>
<pos x="-y" y="-x" z="z+1/2"/>
<pos x="-x+y" y="y" z="z+1/2"/>
<pos x="x" y="x-y" z="z+1/2"/>
</wyck>
<wyck id="2" mul="6" let="e" site=".2">
<pos x="x" y="0" z="1/4"/>
<pos x="0" y="x" z="1/4"/>
<pos x="-x" y="-x" z="1/4"/>
<pos x="-x" y="0" z="3/4"/>
<pos x="0" y="-x" z="3/4"/>
<pos x="x" y="x" z="3/4"/>
</wyck>
<wyck id="3" mul="6" let="d" site="-1">
<pos x="1/2" y="0" z="0"/>
<pos x="0" y="1/2" z="0"/>
<pos x="1/2" y="1/2" z="0"/>
<pos x="0" y="1/2" z="1/2"/>
<pos x="1/2" y="0" z="1/2"/>
<pos x="1/2" y="1/2" z="1/2"/>
</wyck>
<wyck id="4" mul="4" let="c" site="3.">
<pos x="0" y="0" z="z"/>
<pos x="0" y="0" z="-z+1/2"/>
<pos x="0" y="0" z="-z"/>
<pos x="0" y="0" z="z+1/2"/>
</wyck>
<wyck id="5" mul="2" let="b" site="-3.">
<pos x="0" y="0" z="0"/>
<pos x="0" y="0" z="1/2"/>
</wyck>
<wyck id="6" mul="2" let="a" site="32">
<pos x="0" y="0" z="1/4"/>
<pos x="0" y="0" z="3/4"/>
</wyck>
</wyckoff>
</sg-xml>
- "Space-group symmetry," International Tables for Crystallography, vol. A, 2016.