Radial distribution functions fundamentals

The Radial Distribution Function, R.D.F. , g(r), also called pair distribution function or pair correlation function, is an important structural characteristic, therefore computed by Atomes.

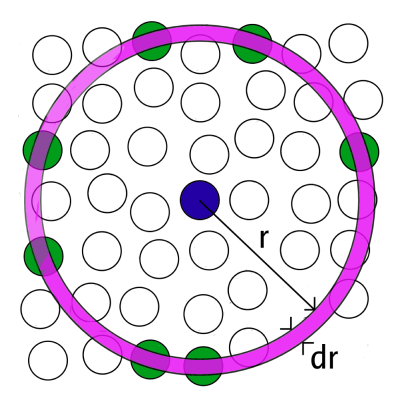
Considering a homogeneous distribution of the atoms/molecules in space, the \(g(r)\) represents the probability to find an atom in a shell \(dr\) at the distance \(r\) of another atom chosen as a reference point [Fig. 5.2]. By dividing the physical space/model volume into shells dr [Fig. 5.2] it is possible to compute the number of atoms \(dn(r)\) at a distance between \(r\) and \(r + dr\) from a given atom: \[\label{g2r_1} dn(r)\ =\ \frac{N}{V}\ g(r)\ 4\pi\ r^{2}\ dr\] where \(N\) represents the total number of atoms, \(V\) the model volume and where \(g(r)\) is the radial distribution function. In this notation the volume of the shell of thickness \(dr\) is approximated: \[\left(V_{\text{shell}}\ =\ \displaystyle{\frac{4}{3}} \pi (r+dr)^3\ -\ \displaystyle{\frac{4}{3}} \pi r^3 \ \simeq\ 4\pi\ r^{2}\ dr \right)\] When more than one chemical species are present the so-called partial radial distribution functions \(g_{\alpha\beta}(r)\) may be computed : \[\label{g2r_4} g_{\alpha \beta}(r)\ =\ \frac{dn_{\alpha \beta}(r)}{4\pi r^{2}\ dr\ \rho_{\alpha}} \qquad \text{with} \qquad \rho_{\alpha}\ =\ \frac{V}{N_\alpha}\ =\ \frac{V}{N\times c_\alpha}\] where \(c_\alpha\) represents the concentration of atomic species \(\alpha\). These functions give the density probability for an atom of the \(\alpha\) species to have a neighbor of the \(\beta\) species at a given distance \(r\). The example features GeS\(_2\) glass.

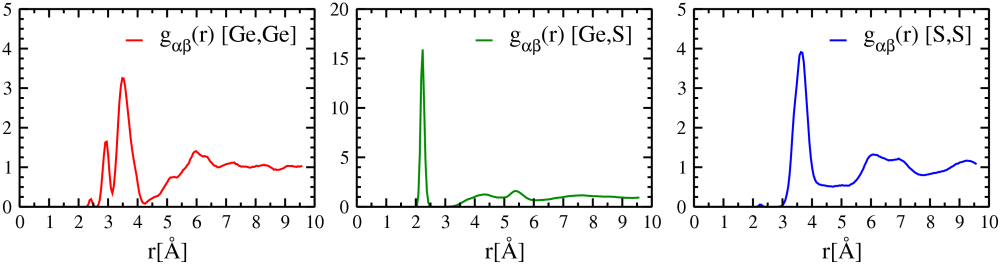
Figure 5.3 shows the partial radial distribution functions for GeS\(_2\) glass at 300 K. The total RDF of a system is a weighted sum of the respective partial RDFs, with the weights depend on the relative concentration and x-ray/neutron scattering amplitudes of the chemical species involved.
It is also possible to use the reduced \({\bf{G}}_{\alpha\beta}(r)\) partial distribution functions defined as: \[{\bf{G}}_{\alpha\beta}(r)\ =\ 4\pi r \rho_0 \left(g_{\alpha \beta}(r)\ - 1\right)\]
Atomes gives access to:

• The partial \(g_{\alpha \beta}(r)\) and \({\bf{G}}_{\alpha\beta}(r)\) distribution functions, and more see [Eq.[s2q_9]].

• The corresponding \(dn_{\alpha \beta}(r)\) integrated number of neighbors.
  

Also two methods are available to compute the radial distribution functions:

• The standard real space calculation typical to analyze 3-dimensional models

• The experiment-like calculation using the Fourier transform of the structure factor obtained using the Debye equation (see section 5.3 for details).