Description of a network using ring

Ring statistics are mainly used to obtain a snapshot of the connectivity of a network. Thereby the better the snapshot will be, the better the description and the understanding of the properties of the material will be. In the literature many papers present studies of materials using ring statistics. In these studies either the number of Rings per Node '\(R_N\)' [1], [2] or the number of Rings per Cell '\(R_C\)' [3], [4], [5] are given as a result of the analysis. The first (\(R_N\)) is calculated for one node by counting all the rings corresponding to the property we are looking for (King's, Guttman's, primitive or strong ring criterion). The second (\(R_C\)) is calculated by counting all the different rings corresponding at least once (at least for one node) to the property we are looking for (King's, shortest path, primitive or strong ring criterion). The values of \(R_N\) and \(R_C\) are often reduced to the number of nodes of the networks. Furthermore the results are presented according to each size of rings.
An example is proposed with a very simple network illustrated in figure 5.19.

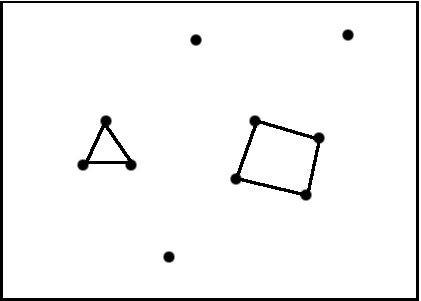
A very simple network.

This network is composed of 10 nodes, arbitrary of the same chemical species, and 7 bonds. Furthermore it is clear that in this network there are 1 ring with 3 nodes and 1 ring with 4 nodes.
It is easy to calculate \(R_N\) and \(R_C\) for the network in figure 5.19 (\(n\) = number of nodes):

Table 5.1: \(R_N\) for the network in figure 5.19
\(n\) \(R_N(n)\)
3 1/10
4 1/10
Table 5.2: \(R_C\) for the network in figure 5.19
\(n\) \(R_C(n)\)
3 3/10
4 4/10


In the literature the values of \(R_N\) and \(R_C\) are usually given separately [1], [2], [3], [4], [5].
Nevertheless these two properties are not sufficient in order to describe a network using rings. A simple example is proposed in figure 5.20.

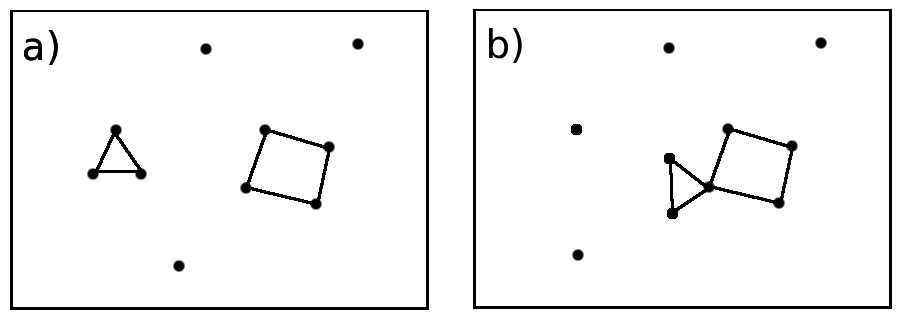
Two simple networks having very close compositions: 10 nodes and 7 links.


The two networks [Fig. 5.20-a] and [Fig. 5.20-b] do have very similar compositions with 10 nodes and 7 links but they are clearly different. Nevertheless the previous definitions of rings per cell and rings per node even taken together will lead to the same description for these two different networks [Tab. 5.3].

Table 5.3: \(R_N\) calculated for the networks illustrated in figure 5.20.
\(n\) \(R_N(n)\)
3 1/10
4 1/10
Table 5.4: \(R_C\) calculated for the networks illustrated in figure 5.20.
\(n\) \(R_C(n)\)
3 3/10
4 4/10


In both cases a) and b) there are 1 ring with 3 nodes and 1 ring with 4 nodes. It has to be noticed that these two rings have properties which correspond to each of the definitions introduced previously (King, Guttman, primitive and strong).
Thus none of these definitions is able to help to distinguish between these two networks. Therefore even though these simple networks are different, the previous definitions lead to the same description.

Thereby it is justified to wonder about the interpretation of the data presented in the literature for amorphous systems with a much higher complexity.

  1. J. P. Rino, I. Ebbsjö, R. K. Kalia, A. Nakano, and P. Vashishta, Phys. Rev. B., vol. 47, no. 6, pp. 3053–3062, 1993.
  2. R. M. Van Ginhoven, H. Jónsson, and L. R. Corrales, Phys. Rev. B., vol. 71, no. 2, p. 024208, 2005.
  3. M. Cobb, D. A. Drabold, and R. L. Cappelletti, Phys. Rev. B., vol. 54, no. 17, pp. 12162–12171, 1996.
  4. X. Zhang and D. A. Drabold, Phys. Rev. B., vol. 62, no. 23, pp. 15695–15701, 2000.
  5. D. N. Tafen and D. A. Drabold, Phys. Rev. B., vol. 71, no. 5, p. 054206, 2005.