Bond defects in ring statistics
ABAB and BABA rings
The ring statistics of amorphous networks are often focused on finding rings made of a succession of atoms with an alternation of chemical species, called ABAB rings. The most common examples come from the alternation of Si and O atoms (in silica polymorphs) or Ge and S (in GeS
The ideal technique to setup the analysis of such systems is to choose the atoms of highest coordination to initiate the search, respectively Si in SiO
![Cluster of atoms isolated from an AB_2 amorphous network. A bond defect is located on an atom of the chemical species B (blue square). When looking for King's shortest paths [S. 5.5.2.1] using the chemical species A to initiate the search the central ring with 10 nodes is ignored. However among the solutions of the analysis (with the initial nodes circled in green) other rings with 10 nodes are found in the network.](/Atomes-doc/img/phys/abba.png)
We can see that this piece of network is characterized by a bond defect. An atom of the B species appears to be over-coordinated by three atoms of the A species. When looking for rings, using the King's criterion [S. 5.5.2.1] and initiating the search using the A atoms, the central ring with 10 nodes is ignored. Nevertheless other rings with 10 nodes are found and stored as solutions of the analysis. In order to find the central ring the search has to be initiated from the overcoordinated B atom.
By analogy with the terminology ABAB this ring can be called a BABA ring. Indeed the alternation of chemical species is well respected. Therefore it is legitimate to question the relevance of the analysis without this result. In other words we have to check out if this BABA ring is, or not, an ABAB ring.
The properties of this ring meet the definition and can therefore improve the description of the connectivity of the network. This kind of coordination defect [Fig. 5.24] is uncommon in vitreous silica [1], [2], nevertheless it is frequent in chalcogenide glasses [3], [4].
Homopolar bonds
In amorphous materials the homopolar bond defects can have a significant influence on the ring statistics. This is true in particular for AB
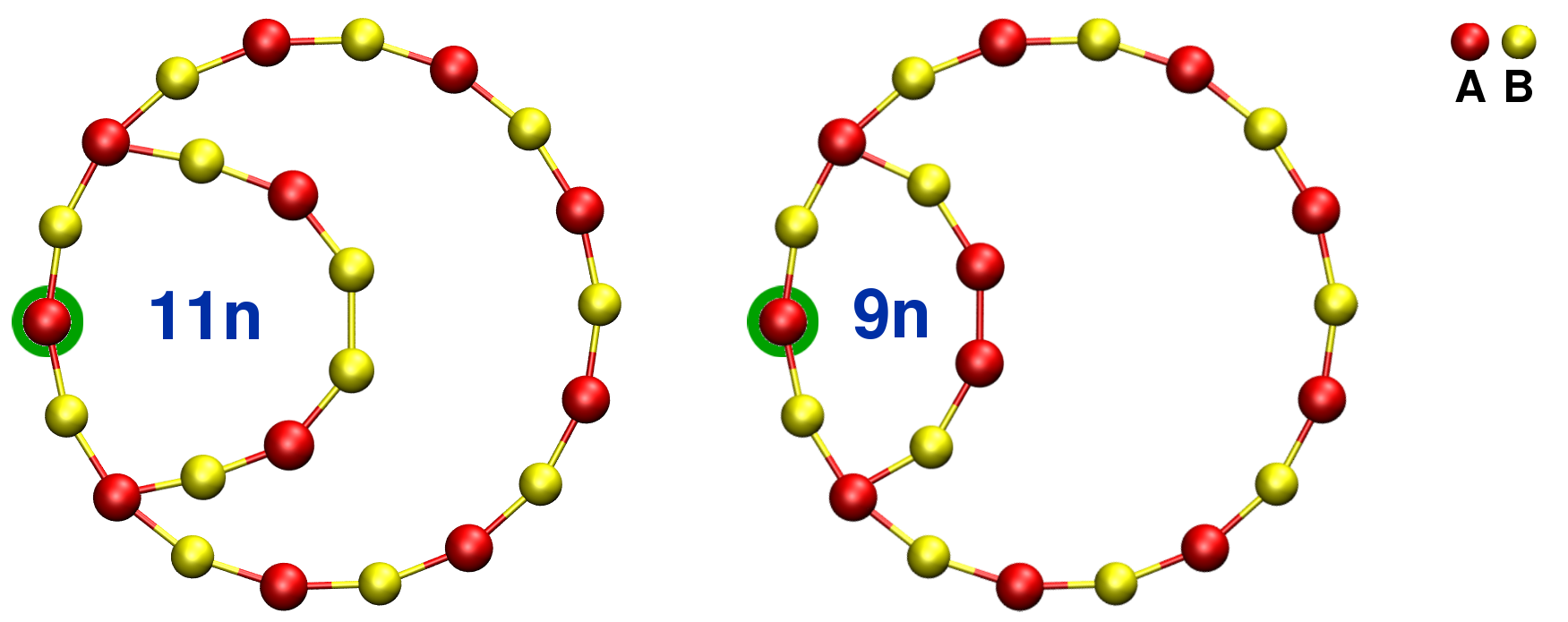
The smallest rings found when initiating the search using the circled nodes (green color) are not ABAB rings. Therefore their size must be given using the total number of nodes. In figure 5.25 the smallest rings are a ring with 9 nodes and a ring with 11 nodes containing respectively an A-A and a B-B homopolar bond. These rings are significantly smaller than the shortest ABAB ring with 18 nodes that may be found when looking for rings using the same green-circled nodes to initiate the analysis [Fig. 5.25].
The Atomes program provides options to take into account or avoid A-B-A-B rings as well as homopolar bonds.
- J. P. Rino, I. Ebbsjö, R. K. Kalia, A. Nakano, and P. Vashishta, Phys. Rev. B., vol. 47, no. 6, pp. 3053–3062, 1993.
- W. Jin, P. Vashishta, R. K. Kalia, and J. P. Rino, Phys. Rev. B., vol. 48, no. 13, pp. 9359–9368, 1993.
- S. Blaineau and P. Jund, Phys. Rev. B., vol. 69, no. 6, p. 064201, 2004.
- S. Le Roux and P. Jund, J. Phys. Cond. Mat., vol. 19, no. 19, p. 169102, 2007.