The periodic boundary conditions

Taking into account the finite size of model/simulation box is crucial to compute correctly many of the structural characteristics (e.g. ring statistics) of the system being studied.
The importance of the finite size of model box can be illustrated using a 1 \(dm^3\) edged cube of water (1 L) at room temperature. This cube contains approximately \(3.3 \times 10^{25}\) water molecules, each of them can be considered as a sphere having a diameter of 2.8 Å. Following this scheme surface interactions can affect up to 10 layers of spheres (water molecules) far from the surface of the model cubic box. In this case the number of water molecules exposed to the surface is about \(2 \times 10^{19}\), which is a small fraction of the total number of molecules in the model.
Currently structure models often contain somewhere from 1 thousand to several thousands of molecules/atoms. As a result a very substantial fraction of them will be influenced by the finite size of the simulation/model box. The problems is solved by applying the so-called Periodic Boundary Conditions "PBC" which means surrounding the simulation box with its translational images in the 3 directions of space, as illustrated below.
Users of Atomes should take special care that their model boxes are inherently periodic so that when the periodic boundary conditions are applied the structural characteristics computed are not compromised.

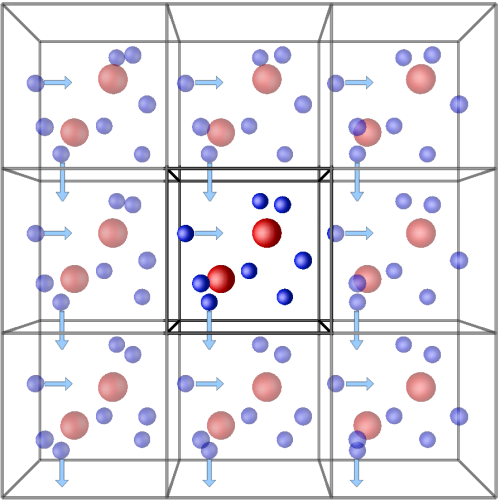
**Figure 5.1:** Schematic representation of the idea of periodic boundary conditions.

Figure 5.1 illustrates the principle of the periodic boundary conditions that can be used¹ in Atomes: a particle which goes out from the simulation box by one side is reintroduced in the box by the opposite side (in the 3 dimensions of space).
When PBC are used the maximum inter-atomic distance r\(_{max}\) which is taken into account in the calculations, depends on the lattice parameters: \[r_{max} \simeq \frac{L\times\sqrt{3}}{2}\qquad \text{with}\ L = \text{box size}\] The surface/finite model size effects would therefore be small, if any. In general, the larger the simulation box and the number of molecules/atoms in it, the smaller the surface/size effects will be.

Please note that the use of PBC is not mandatory, isolated molecules can be studied using Atomes↩︎